Can You Defeat the Detroit Lines?

This week’s Riddler Express features a challenge drawn from the world of football analytics:

In the Riddler Football League, you are coaching the Arizona Ordinals against your opponent, the Detroit Lines, and your team is down by 14 points. You can assume that you have exactly two remaining possessions (i.e., opportunities to score), and that Detroit will score no more points.

For those unfamiliar with American football, a touchdown is worth 6 points. After each touchdown, you can decide whether to go for 1 extra point or 2 extra points. You happen to have a great kicker on your team, and your chances of scoring 1 extra point (should you go for it) are 100 percent. Meanwhile, scoring 2 extra points is no sure thing — suppose that your team’s probability of success is some value p.

If the teams are tied at the end of regulation, the game proceeds to overtime, which you have a 50 percent chance of winning. (Assuming ties are not allowed.)

What is the minimum value of p such that you’d go for 2 extra points after your team’s first touchdown (i.e., when you’re down 8 points)?

To solve the problem, we need to know the probability of victory conditional on all possible outcomes. There are two separate events (i.e. two possessions to potentially score one or two points). We define the probability of these individual events as

\begin{aligned} \Pr (\text{2PT conversion}) = p \\ \Pr (\text{extra point}) = 1 \end{aligned}

Given the assumptions, we know an extra point will be successful 100% of the time, whereas two-point conversions are only successful with probability \(p\). If we choose the extra point, we can kick another extra point on the second possession and have a 50% chance of victory in overtime. That is our baseline for success - we need \(p\) to be sufficiently high that the probability of victory is greater than 50%.

If we go for two points in the first possession, we will either successfully attempt a two-point conversion with probability \(p\), or fail to attempt a two-point conversion with probability \(1-p\). If we are successful on the conversion, we are guaranteed victory (all we need to do on the second possession is kick an extra point). So the conditional probability of victory \(\Pr (\text{Victory} | \text{2PT conversion}) = 1\).

What if we fail on the first attempt? We can still attempt a two-point conversion on the second possession. If successful, the game will go to overtime where we still have a 50% chance of victory. So we can define this conditional probability \(\Pr (\text{Victory} | \text{2PT conversion fails}) = p \times 0.5\).

To determine the overall probability of victory if we attempt a two-point conversion on the first possession, we use the law of total probability to combine the conditional probabilities of victory weighted by the probability that each event occurs.

\begin{aligned} \Pr(\text{Victory}) &= 1 \times p + (p \times 0.5) \times (1 - p) \\ &= p + 0.5 p (1 - p) \\ &= p + 0.5p - 0.5 p^2 \\ &= 1.5 p - 0.5 p^2 \\ &= p (1.5 - .5p) \end{aligned}

At this point, all we need to do is find the minimum value for \(p\) such that \(\Pr (\text{Victory}) > 0.5\). We could solve this analytically, but it’s also trivial to determine computationally.

# define function for probability of victory
p_win <- function(p) 1.5 * p - .5 * p^2

# evaluate function at a range of values for p
p <- seq(from = 0, to = 1, by = 0.001)
p_win_out <- p_win(p)

# which p is just above .5?
p[[which.min(abs(p_win_out - .5))]]

## [1] 0.382

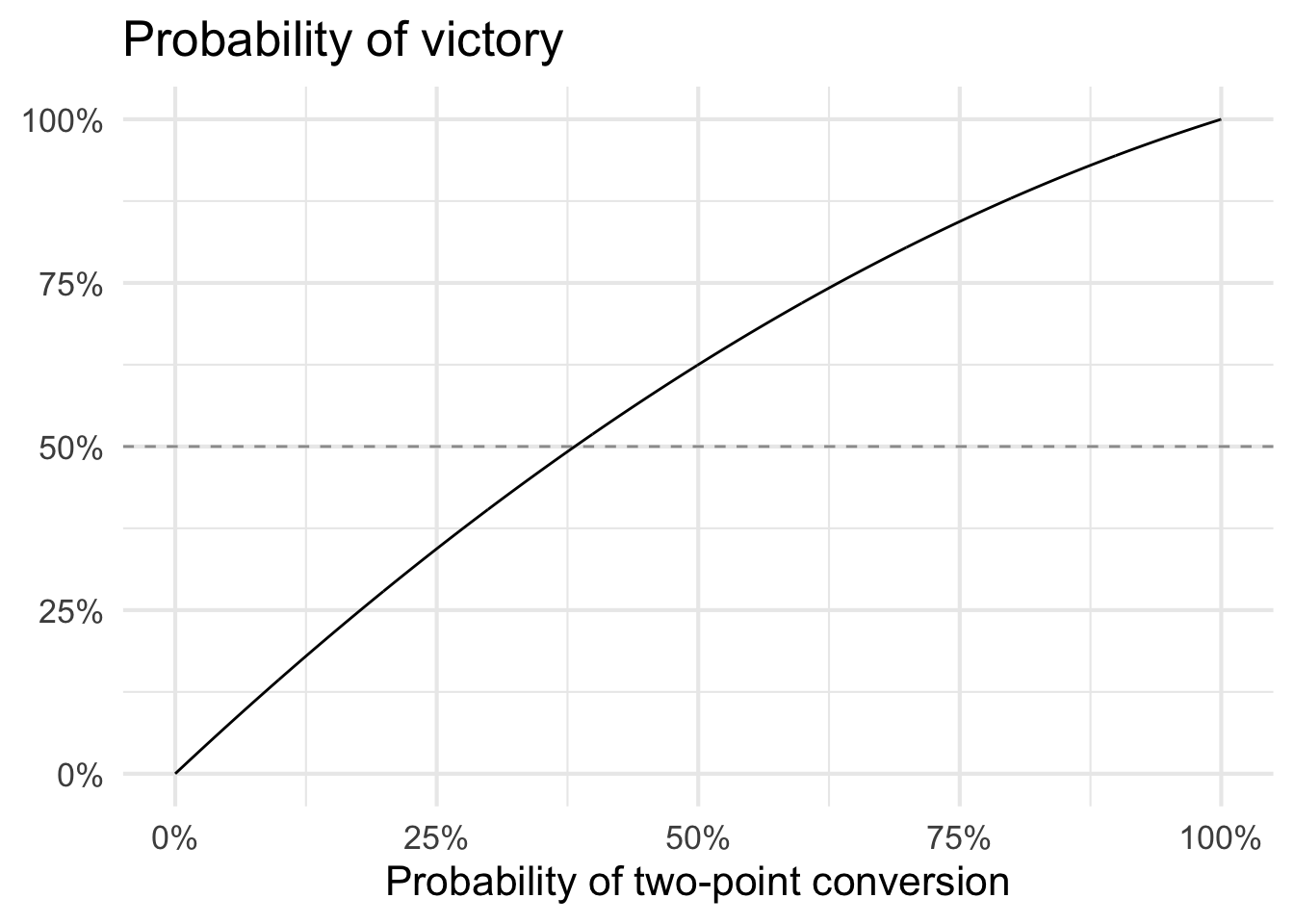
Figure 1: Probability of victory based on different two-point conversion success rates

Any \(p \geq 0.382\) gives us a higher probability of victory than kicking extra points and hoping for victory in overtime. Considering the league average two-point conversion rate, it’s not surprising more teams are going for two in these types of situations.