Time travel for the lottery
By Benjamin Soltoff in R
October 10, 2021
Today’s Riddler Express features an interesting optimization problem:
Channeling your inner Marty McFly, you travel one week back in time in an attempt to win the lottery. It’s worth $10 million, and each ticket costs a dollar. Note that if you win, your ticket purchase is not refunded. All of this sounds pretty great.
The problem is, you’re not alone. There are 10 other time travelers who also know the winning numbers. You know for a fact that each of them will buy exactly one lottery ticket. Now, according to the lottery’s rules, the prize is evenly split among all the winning tickets (i.e., not evenly among winning people). How many tickets should you buy to maximize your profits?
Our profits are defined as
\begin{aligned} \text{Profits} &= \frac{\text{Lottery Prize}}{\text{Number of tickets I purchase} + \text{Other winning tickets}} \times \text{Number of tickets I purchase} \\ &\quad - (\text{Number of tickets I purchase} \times \text{Ticket cost}) \end{aligned}
This accounts for my lottery payout minus the expense of purchasing all my tickets. For this specific formulation, the equation simplifies to
\begin{equation} \text{Profits} = \frac{10{,}000{,}000}{\text{Tickets} + 10} \times \text{Tickets} - \text{Tickets} \end{equation}
where \(\text{Tickets}\) is the quantity of tickets I purchase. Since each ticket is $1, the second term is simply \(\text{Tickets}\).
We can optimize this using an optimizer function in R. However since we only have \(10{,}000{,}000\) possible number of tickets to purchase (anything greater than that would result in a net loss) we can just perform a grid search.1
library(tidyverse)
theme_set(theme_minimal(base_size = 16))
# earnings function
lottery_earnings <- function(my_tickets = 1, lottery_prize = 1e07, other_tickets = 10){
# earnings per ticket
per_ticket_earnings <- lottery_prize / (my_tickets + other_tickets)
# total payout i receive
payout <- per_ticket_earnings * my_tickets
# subtract how much i spent on tickets
net_earnings <- payout - my_tickets
return(net_earnings)
}
# calculate all possible earnings
earnings_tbl <- tibble(
my_tickets = seq(from = 1, to = 1e07, by = 1),
net_earnings = lottery_earnings(my_tickets = my_tickets)
)
Table: Table 1: Optimal number of tickets to purchase
| Number of tickets purchased | Net earnings |
|---|---|
| 9,990 | $9,980,010 |
| 9,991 | $9,980,010 |
| 9,989 | $9,980,010 |
| 9,992 | $9,980,010 |
| 9,988 | $9,980,010 |
| 9,993 | $9,980,010 |
| 9,987 | $9,980,010 |
| 9,994 | $9,980,010 |
| 9,986 | $9,980,010 |
| 9,995 | $9,980,010 |
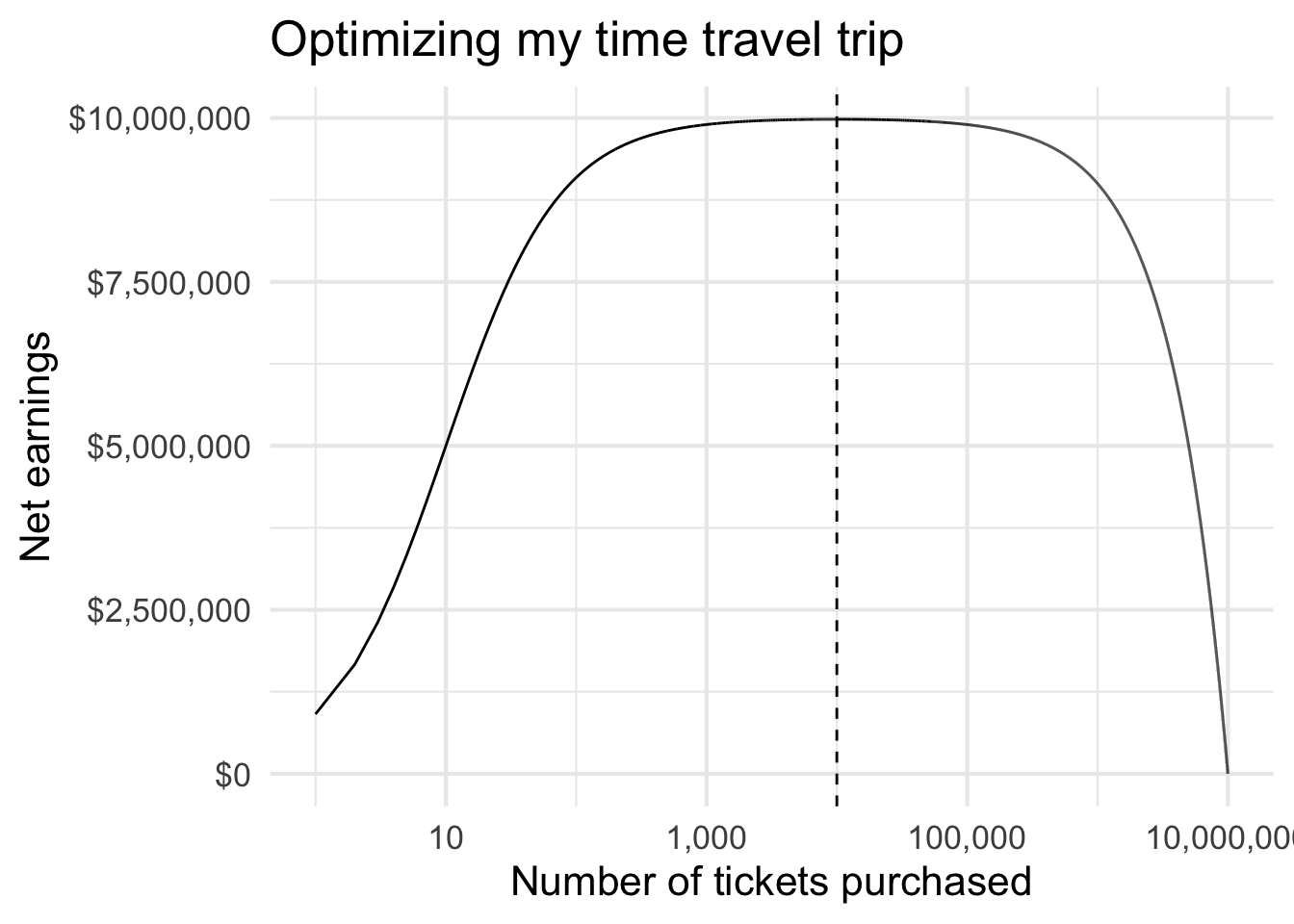
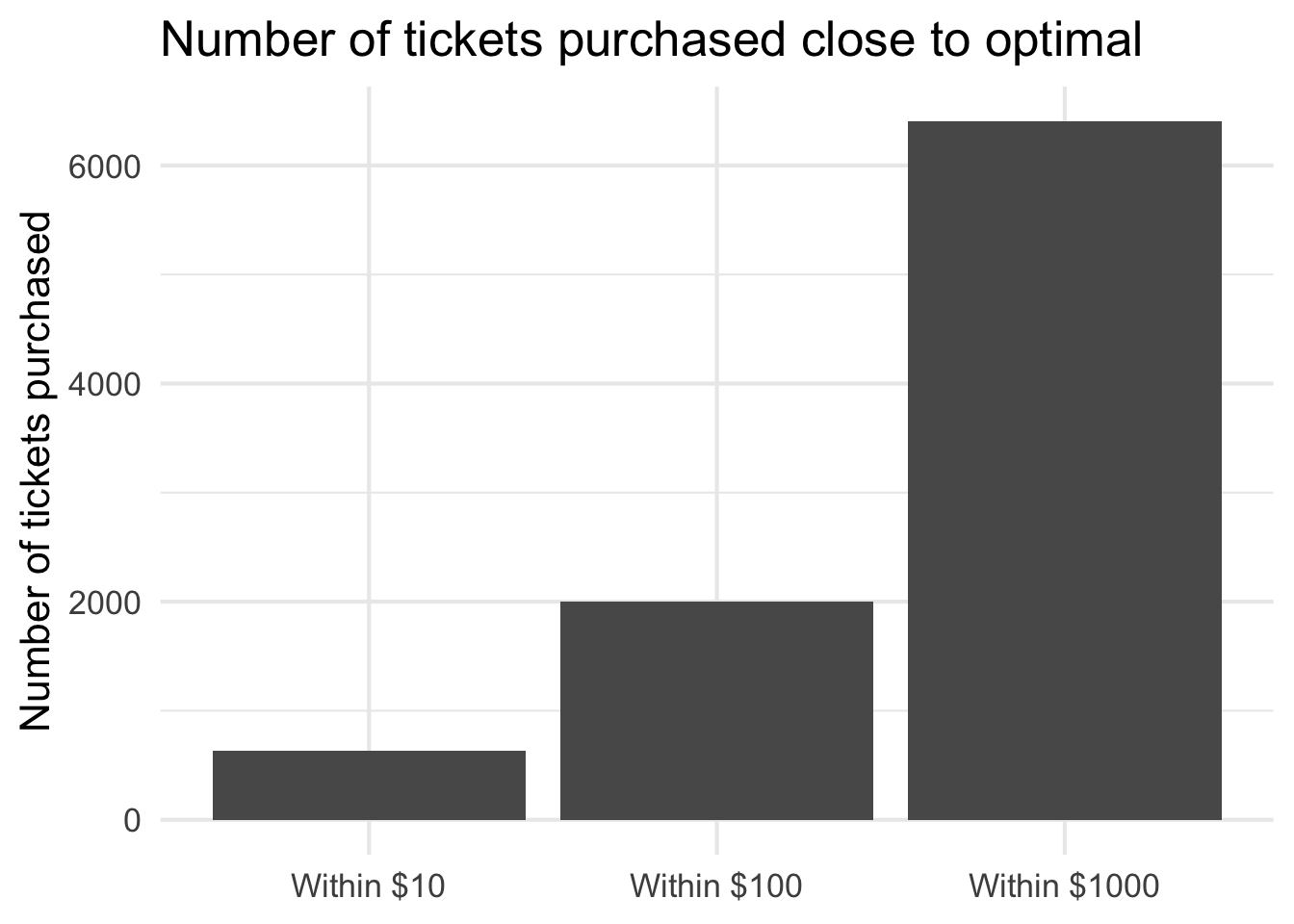
9,990 is the optimal number of tickets to purchase. Anything less than that and our net earnings will be lower than the maximum. Anything more than that is wasted money. Though to be fair, there is a clear plateau where some quantities of tickets are within the optimal net earnings.
-
Technically we would be guaranteed to lose money after
\(9{,}999{,}990\)since we know 10 other winning tickets were purchased. ↩︎