How Good Are You At Guess Who?
in r
March 8, 2020
The most recent Riddler Express gave me an opportunity to refresh some base R notation, as well as combine it with a technique I learned while reading Hadley Wickham’s Advanced R. The challenge is:
A local cafe has board games on a shelf, designed to keep kids (and some adults) entertained while they wait on their food. One of the games is a tic-tac-toe board, which comes with nine pieces that you and your opponent can place: five Xs and four Os.
When I took my two-year-old with me, he wasn’t particularly interested in the game itself, but rather in the placement of the pieces.
If he randomly places all nine pieces in the nine slots on the tic-tac-toe board (with one piece in each slot), what’s the probability that X wins? That is, what’s the probability that there will be at least one occurrence of three Xs in a row at the same time there are no occurrences of three Os in a row?
My first thought was that a tic-tac-toe board can be represented as a matrix. If any of the columns or rows or diagonals of the matrix contain three Xs while simultaneously not containing any Os, X wins.
I don’t typically work with matrix structures in R (more often my work involves data frames), but this proved to be a nice refresher. My first approach was to simulate \(N\) games of tic-tac-toe by random sampling from the set of Xs and Os. Then I remembered teaching permutations in
a statistics class last year. Why not consider all possible outcomes and calculate the winner? There are
$$\frac{n!}{(n - k)!}$$
possible outcomes, where we choose \(k\) objects from a set of \(n\) objects. In this instance, we consider
$$\frac{9!}{(9-9)!} = \frac{9!}{0!}$$
where by definition \(0! = 1\). So we have 362,880 possible outcomes. We can generate all those possible outcomes using gtools::permutations(). In order to use this function, each value in the vector to permute must be unique. So I represent each value uniquely, then after I generate all possible permutations represent the Xs as \(+1\) and the Os as \(-1\).
library(tidyverse)
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
## ✓ ggplot2 3.3.3 ✓ purrr 0.3.4
## ✓ tibble 3.1.1 ✓ dplyr 1.0.6
## ✓ tidyr 1.1.3 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()
set.seed(123)
theme_set(theme_minimal(base_size = 18))
pieces <- c(rep(1, times = 5), rep(-1, times = 4))
all_outcomes <- gtools::permutations(n = length(pieces), r = length(pieces), v = seq_along(pieces))
head(all_outcomes)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 1 2 3 4 5 6 7 8 9
## [2,] 1 2 3 4 5 6 7 9 8
## [3,] 1 2 3 4 5 6 8 7 9
## [4,] 1 2 3 4 5 6 8 9 7
## [5,] 1 2 3 4 5 6 9 7 8
## [6,] 1 2 3 4 5 6 9 8 7
# 1:5 = X, 6:9 = O
all_outcomes[all_outcomes <= 5] <- 1
all_outcomes[all_outcomes > 5] <- -1
head(all_outcomes)
## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
## [1,] 1 1 1 1 1 -1 -1 -1 -1
## [2,] 1 1 1 1 1 -1 -1 -1 -1
## [3,] 1 1 1 1 1 -1 -1 -1 -1
## [4,] 1 1 1 1 1 -1 -1 -1 -1
## [5,] 1 1 1 1 1 -1 -1 -1 -1
## [6,] 1 1 1 1 1 -1 -1 -1 -1
Next I wrote a function that takes a single permutation as its input, turns it into a matrix, and checks to see if there are three Xs in any row, column, or diagonal. Since diag() only returns the diagonal of a matrix and I also need to evaluate the diagonal running from bottom to top, I use the rotate() function1 to turn the game board 90 degrees - this allows me to use the diag() function to obtain the same results.
# function to rotate a matrix 90 degrees to check the other diagonal
rotate <- function(x) t(apply(x, 2, rev))
# function to evaluate the outcome of the game
tic_tac_toe <- function(game_board, print_board = FALSE) {
# generate random assortment
game_board <- matrix(data = game_board, nrow = 3)
if (print_board) print(game_board)
# check if any row or colsums or diag or inverse diag are 3
# if TRUE, also confirm none are -3
if (3 %in% colSums(game_board) ||
3 %in% rowSums(game_board) ||
sum(diag(game_board)) == 3 ||
sum(diag(rotate(game_board))) == 3) {
if (-3 %in% colSums(game_board) ||
-3 %in% rowSums(game_board) ||
sum(diag(game_board)) == -3 ||
sum(diag(rotate(game_board))) == -3) {
return("Draw")
}
return("X wins")
} else if (-3 %in% colSums(game_board) ||
-3 %in% rowSums(game_board) ||
sum(diag(game_board)) == -3 ||
sum(diag(rotate(game_board))) == -3) {
return("O wins")
} else {
return("Draw")
}
}
tic_tac_toe(all_outcomes[1, ], print_board = TRUE) # test the function
## [,1] [,2] [,3]
## [1,] 1 1 -1
## [2,] 1 1 -1
## [3,] 1 -1 -1
## [1] "Draw"
Now that I know the function works, I need to apply it to all possible outcomes. Since all_outcomes is structured as a matrix, an apply() function would be appropriate here. The problem is I have not used apply() in years, and I am biased towards purrr::map() functions. Typically map() cannot be used on a matrix input. However,
purrr includes a handy function called array_branch() which converts a matrix to a list object that can then be mapped over.
all_outcomes <- tibble(
outcome = array_branch(all_outcomes, 1),
result = map_chr(outcome, tic_tac_toe)
)
all_outcomes
## # A tibble: 362,880 x 2
## outcome result
## <list> <chr>
## 1 <dbl [9]> Draw
## 2 <dbl [9]> Draw
## 3 <dbl [9]> Draw
## 4 <dbl [9]> Draw
## 5 <dbl [9]> Draw
## 6 <dbl [9]> Draw
## 7 <dbl [9]> Draw
## 8 <dbl [9]> Draw
## 9 <dbl [9]> Draw
## 10 <dbl [9]> Draw
## # … with 362,870 more rows
So what are the results? What is the probability X wins?
all_outcomes_sum <- all_outcomes %>%
count(result) %>%
mutate(prop = n / sum(n))
ggplot(
data = all_outcomes_sum,
mapping = aes(x = fct_reorder(result, -prop), y = prop)
) +
geom_col() +
scale_y_continuous(labels = scales::percent) +
labs(
title = "Probability of each outcome in tic-tac-toe",
x = NULL,
y = NULL
)
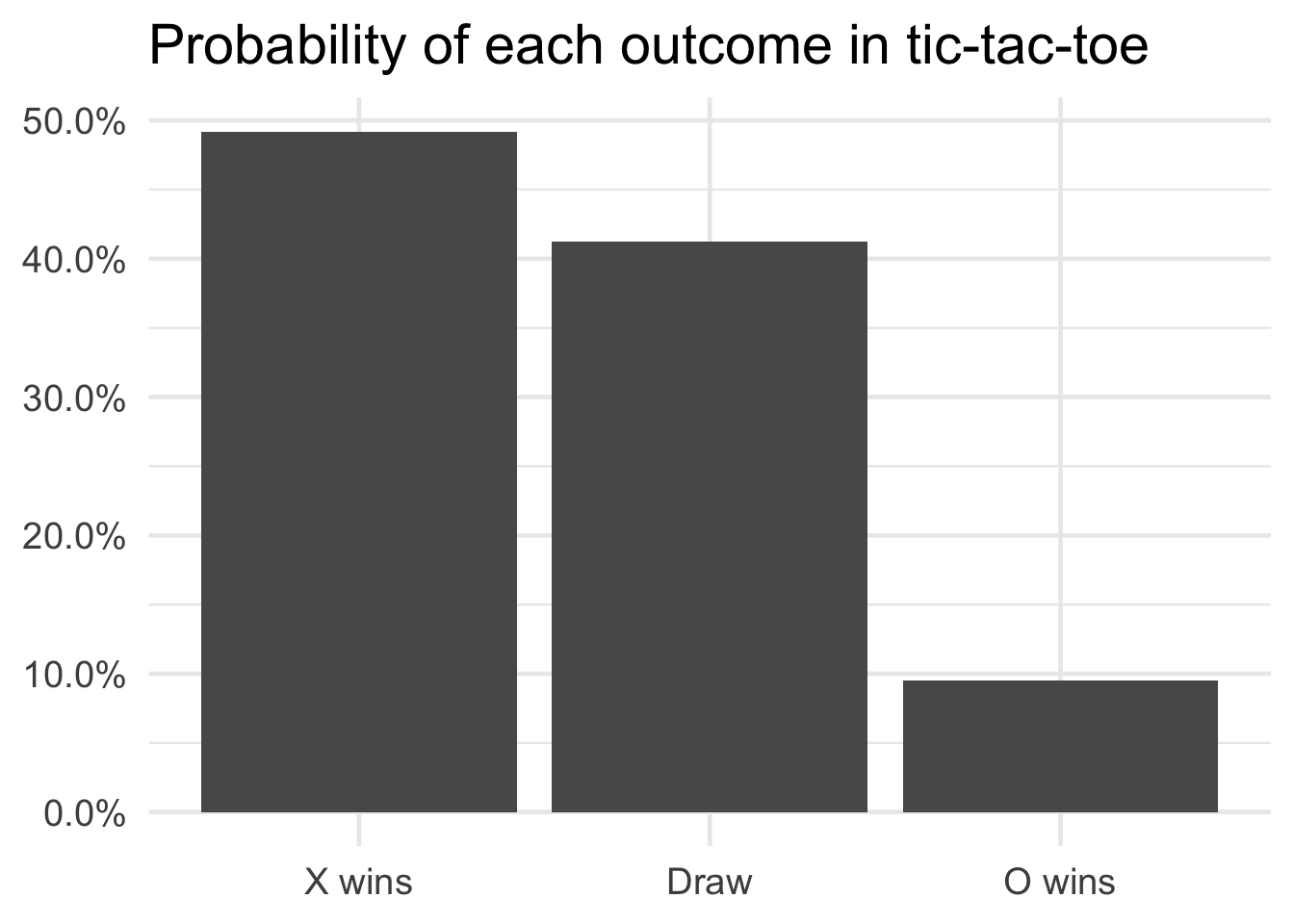
Overall, X wins approximately 49.2% of all possible matches. A draw is the next most likely outcome, whereas O’s probability of success is a measly 9.5%. First-mover advantage is strong here. Of course, we also know the only winning move is not to play.
Session Info
devtools::session_info()
## ─ Session info ───────────────────────────────────────────────────────────────
## setting value
## version R version 4.0.4 (2021-02-15)
## os macOS Big Sur 10.16
## system x86_64, darwin17.0
## ui X11
## language (EN)
## collate en_US.UTF-8
## ctype en_US.UTF-8
## tz America/Chicago
## date 2021-06-01
##
## ─ Packages ───────────────────────────────────────────────────────────────────
## package * version date lib source
## assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.0.0)
## backports 1.2.1 2020-12-09 [1] CRAN (R 4.0.2)
## blogdown 1.3 2021-04-14 [1] CRAN (R 4.0.2)
## bookdown 0.22 2021-04-22 [1] CRAN (R 4.0.2)
## broom 0.7.6 2021-04-05 [1] CRAN (R 4.0.4)
## bslib 0.2.5 2021-05-12 [1] CRAN (R 4.0.4)
## cachem 1.0.5 2021-05-15 [1] CRAN (R 4.0.2)
## callr 3.7.0 2021-04-20 [1] CRAN (R 4.0.2)
## cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.0.0)
## cli 2.5.0 2021-04-26 [1] CRAN (R 4.0.2)
## colorspace 2.0-1 2021-05-04 [1] CRAN (R 4.0.2)
## crayon 1.4.1 2021-02-08 [1] CRAN (R 4.0.2)
## DBI 1.1.1 2021-01-15 [1] CRAN (R 4.0.2)
## dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.0.4)
## desc 1.3.0 2021-03-05 [1] CRAN (R 4.0.2)
## devtools 2.4.1 2021-05-05 [1] CRAN (R 4.0.2)
## digest 0.6.27 2020-10-24 [1] CRAN (R 4.0.2)
## dplyr * 1.0.6 2021-05-05 [1] CRAN (R 4.0.2)
## ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.0.2)
## evaluate 0.14 2019-05-28 [1] CRAN (R 4.0.0)
## fansi 0.4.2 2021-01-15 [1] CRAN (R 4.0.2)
## fastmap 1.1.0 2021-01-25 [1] CRAN (R 4.0.2)
## forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.0.2)
## fs 1.5.0 2020-07-31 [1] CRAN (R 4.0.2)
## generics 0.1.0 2020-10-31 [1] CRAN (R 4.0.2)
## ggplot2 * 3.3.3 2020-12-30 [1] CRAN (R 4.0.2)
## glue 1.4.2 2020-08-27 [1] CRAN (R 4.0.2)
## gtable 0.3.0 2019-03-25 [1] CRAN (R 4.0.0)
## haven 2.4.1 2021-04-23 [1] CRAN (R 4.0.2)
## here 1.0.1 2020-12-13 [1] CRAN (R 4.0.2)
## hms 1.1.0 2021-05-17 [1] CRAN (R 4.0.4)
## htmltools 0.5.1.1 2021-01-22 [1] CRAN (R 4.0.2)
## httr 1.4.2 2020-07-20 [1] CRAN (R 4.0.2)
## jquerylib 0.1.4 2021-04-26 [1] CRAN (R 4.0.2)
## jsonlite 1.7.2 2020-12-09 [1] CRAN (R 4.0.2)
## knitr 1.33 2021-04-24 [1] CRAN (R 4.0.2)
## lifecycle 1.0.0 2021-02-15 [1] CRAN (R 4.0.2)
## lubridate 1.7.10 2021-02-26 [1] CRAN (R 4.0.2)
## magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.0.2)
## memoise 2.0.0 2021-01-26 [1] CRAN (R 4.0.2)
## modelr 0.1.8 2020-05-19 [1] CRAN (R 4.0.0)
## munsell 0.5.0 2018-06-12 [1] CRAN (R 4.0.0)
## pillar 1.6.1 2021-05-16 [1] CRAN (R 4.0.4)
## pkgbuild 1.2.0 2020-12-15 [1] CRAN (R 4.0.2)
## pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.0.0)
## pkgload 1.2.1 2021-04-06 [1] CRAN (R 4.0.2)
## prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.0.0)
## processx 3.5.2 2021-04-30 [1] CRAN (R 4.0.2)
## ps 1.6.0 2021-02-28 [1] CRAN (R 4.0.2)
## purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.0.0)
## R6 2.5.0 2020-10-28 [1] CRAN (R 4.0.2)
## Rcpp 1.0.6 2021-01-15 [1] CRAN (R 4.0.2)
## readr * 1.4.0 2020-10-05 [1] CRAN (R 4.0.2)
## readxl 1.3.1 2019-03-13 [1] CRAN (R 4.0.0)
## remotes 2.3.0 2021-04-01 [1] CRAN (R 4.0.2)
## reprex 2.0.0 2021-04-02 [1] CRAN (R 4.0.2)
## rlang 0.4.11 2021-04-30 [1] CRAN (R 4.0.2)
## rmarkdown 2.8 2021-05-07 [1] CRAN (R 4.0.2)
## rprojroot 2.0.2 2020-11-15 [1] CRAN (R 4.0.2)
## rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.0.2)
## rvest 1.0.0 2021-03-09 [1] CRAN (R 4.0.2)
## sass 0.4.0 2021-05-12 [1] CRAN (R 4.0.2)
## scales 1.1.1 2020-05-11 [1] CRAN (R 4.0.0)
## sessioninfo 1.1.1 2018-11-05 [1] CRAN (R 4.0.0)
## stringi 1.6.1 2021-05-10 [1] CRAN (R 4.0.2)
## stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.0.0)
## testthat 3.0.2 2021-02-14 [1] CRAN (R 4.0.2)
## tibble * 3.1.1 2021-04-18 [1] CRAN (R 4.0.2)
## tidyr * 1.1.3 2021-03-03 [1] CRAN (R 4.0.2)
## tidyselect 1.1.1 2021-04-30 [1] CRAN (R 4.0.2)
## tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.0.2)
## usethis 2.0.1 2021-02-10 [1] CRAN (R 4.0.2)
## utf8 1.2.1 2021-03-12 [1] CRAN (R 4.0.2)
## vctrs 0.3.8 2021-04-29 [1] CRAN (R 4.0.2)
## withr 2.4.2 2021-04-18 [1] CRAN (R 4.0.2)
## xfun 0.23 2021-05-15 [1] CRAN (R 4.0.2)
## xml2 1.3.2 2020-04-23 [1] CRAN (R 4.0.0)
## yaml 2.2.1 2020-02-01 [1] CRAN (R 4.0.0)
##
## [1] /Library/Frameworks/R.framework/Versions/4.0/Resources/library
-
Hat tip to Stack Overflow ↩︎